Introduction to Mechanisms
Yi Zhang
with
Susan Finger
Stephannie Behrens
This chapter introduces the basic physical principles behind
mechanisms as well as basic concepts and principles required for this
course.
Force: an agent or influence that, if applied to a free
body results chiefly in an acceleration of the body and sometimes in
elastic deformation and other effects.
Every day we deal with forces of one kind or another. A
pressure is a force. The earth exerts a force of attraction for all
bodies or objects on its surface. To study the forces acting on
objects, we must know how the forces are applied, the direction of the
forces and their value. Graphically, forces are often represented by a
vector whose end represents the point of action.
A mechanism is what is responsible for any action or reaction.
Machines are based on the idea of transmitting forces through a
series of predetermined motions. These related concepts are the
basis of dynamic movement.
Torque: Something that produces or tends to produce rotation
and whose effectiveness is measured by the product of the force and
the perpendicular distance from the line of action of the force to the
axis of rotation.
Consider the lever shown in Figure 1-1. The lever
is a bar that is free to turn about the fixed point, A, called the
fulcrum; a weight acts on the one side of the lever, and a balancing
force acts on the other side of the lever.
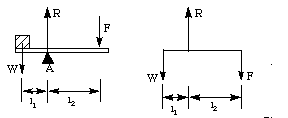
Figure 1-1 A lever with balanced forces
To analyze levers, we need to find the torques of the
forces acting on the lever. To get the torque of force W about
point A, multiply W by l1, its distance from
A. Similarly F x l2 is the torque of F about
fulcrum A.
Motion: a change of position or orientation.
We begin our study of motion with the simplest case, motion in a
straight line.
- Position and displacement along a line
The first step in the study of motion is to describe the position of a
moving object. Consider a car on an east-west stretch of straight
highway. We can describe the displacement of the car by
saying "the car is 5 kilometers west of the center town". In this
description, we specified two factors, the original point of measure
and the direction of the displacement.
- Velocity
We can define the velocity of an object moving steadily
as its displacement per unit time:
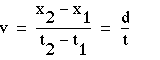
(1-1)
where t = t2 - t1 is the time interval during which the displacement
occurred. When velocity varies, we can let the time interval become
infinitesimally small, thus
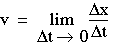
(1-2)
- Acceleration
Acceleration is the variation of the velocity in a unit time
period. If the velocity changes in a constant rate, then we can
describe the acceleration by
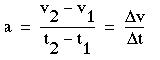
(1-3)
More generally, acceleration is
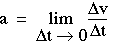
(1-4)
The picture becomes more complicated when the motion is not merely
along a straight line, but rather extends into a plane. Here we
can describe the motion with a vector which includes the magnitude and
the direction of movement.
- Position vector and displacement vector
The directed segment which describes the position of an object
relative to an origin is the position vector, as
d1 and d2 in Figure
1-2
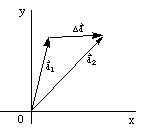
Figure 1-2 Position vector and displacement vector
If we wish to describe a motion from position d1 to
position d2, for example, we can use vector
d1, the vector starts at the point described by
d1 and goes to the point described by
d2, which is called the displacement vector.
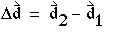
(1-5)
- Velocity vector
For a displacement  d occurring in a
time interval d occurring in a
time interval  t, the
average velocity during the interval is t, the
average velocity during the interval is
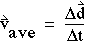
(1-6)
Clearly Vave has the direction of  d. d.
In the limit as delta t approaches zero, the instantaneous velocity is
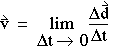
(1-7)
The direction of V is the direction of  d for a very small
displacement; it is therefore along, or tangent to, the path. d for a very small
displacement; it is therefore along, or tangent to, the path.
- Acceleration vector
The instantaneous acceleration is the limit of the ratio  V/ V/ t as t as  t becomes very small: t becomes very small:
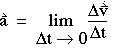 (1-8) (1-8)
The previous sections discuss the motion of particles. For a rigid
body in a plane, its motion is often more complex than a particle
because it is comprised of a linear motion and a rotary
motion. Generally, this kind of motion can be decomposed into two
motions (Figure 1-3), they are:
- The linear motion of the center of the mass of the rigid body. In
this part of the motion, the motion is the same as the motion of a
particle on a plane.
- The rotary motion of the rigid body relative
to its center of mass.
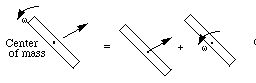
Figure 1-3 Motion of a rigid body in a plane
When no force is exerted on a body, it stays at rest or moves in a
straight line with constant speed. This principle of inertia is also
known as Newton's first law. It is from this law that
Newton was able to build up our present understanding of dynamics.
From our daily life, we can can observe that: - When a
force F is applied on an object,
 V, the change of
the velocity of the object, increases with the length of time delta t
increases; V, the change of
the velocity of the object, increases with the length of time delta t
increases;
- The greater the force F, the greater
 V; and V; and
- The larger the body (object) is, the less easily accelerated by forces.
It is convenient to write the proportionality between F t and t and  V in the form: V in the form:
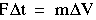 (1-9) (1-9)
The proportionality constant m varies with the object. This
constant m is refered to as the inertial mass of
the body. The relationship above embodies Newton's law of
motion (Newton's second law). As
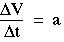 (1-10) (1-10)
in which a is the acceleration of the object. We have
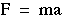 (1-11) (1-11)
If m = 1 kg and a = 1m/sec2, than F = 1
newton.
Forces and accelerations are vectors, and Newton's law can be written
in vector form.
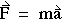 (1-12) (1-12)
Try to make a baseball and a cannon ball roll at the same speed.
As you can guess, it is harder to get the cannon ball going. If you
apply a constant force F for a time  t, the change in velocity
is given by Equation 1-9. So, to get the same t, the change in velocity
is given by Equation 1-9. So, to get the same
 v, the
product F v, the
product F t
must be greater the greater the mass m you are trying to accelerate. t
must be greater the greater the mass m you are trying to accelerate.
To throw a cannon ball from rest and give it the same final velocity
as a baseball (also starting from rest), we must push either harder or
longer. What counts is the product F t. This product
F t. This product
F t is the
natural measure of how hard and how long we push to change a
motion. It is called the impulse of the force. t is the
natural measure of how hard and how long we push to change a
motion. It is called the impulse of the force.
Suppose we apply the same impulse to a baseball and a cannon
ball, both initially at rest. Since the initial value of the quantity
mv is zero in each case, and since equal impulses are
applied, the final values mv will be equal for the baseball and
the cannon ball. Yet, because the mass of the cannon ball is much
greater than the mass of the baseball, the velocity of the cannon ball
will be much less than the velocity of the baseball. The product
mv, then, is quite a different measure of the motion
than simply v alone. We call it the momentum
p of the body, and measure it in kilogram-meters per second.
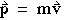 (1-13) (1-13)
Velocity and momentum are quite
different concepts: velocity is a kinematical quantity, whereas
momentum is a dynamic one, connected with the causes of changes
in the motion of masses.
Because of its connection with the impulse
which occurs naturally in Newton's law (Equation 1-9), we expect
momentum to fit naturally into Newtonian dynamics. Newton did
express his law of motion in terms of the momentum, which he
called the quantity of motion. We can express Newton's law in
terms of the change in momentum instead of change in
velocity:
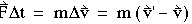 (1-14) (1-14)
where v and v' are the velocities before and after the
impulse. The right-hand side of the last equation can be written as
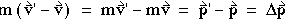 (1-15) (1-15)
the change in the momentum. Therefore
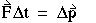 (1-16) (1-16)
or, in other words, the impulse equals the change in the
momentum.
In Figure 1-4 a moving billiard ball collides
with a billiard ball at rest. The incident ball stops and the ball it
hits goes off with the same velocity with which the incident ball came
in. The two billiard balls have the same mass. Therefore, the momentum of the second ball after the
collision is the same as that of the incident ball before
collision. The incident ball has lost all its momentum, and the
ball it struck has gained exactly the momentum which the
incident ball lost.
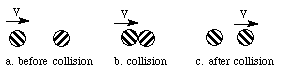
Figure 1-4 Collision of billiard balls
This phenomenon is consistent with the law of conservation of
momentum which says that the total momentum is constant
when two bodies interact.
Work is a force applied over a distance. If you drag an
object along the floor you do work in overcoming the friction
between the object and the floor. In lifting an object you do
work against gravity which tends to pull the object toward the
earth. Steam in a locomotive cylinder does work when it expands
and moves the piston against the resisting forces. Work
is the product of the resistance overcome and the distance through
which it is overcome.
Power is the rate at which work is done.
In the British system, power is expressed in foot-pounds per second.
For larger measurements, the horsepower is used.
1horsepower = 550ft *lb/s = 33,000ft*lb/min
In SI units, power is measured in joules per second, also called
the watt (W).
1hp = 746 W = 0.746kW
All object possess energy. This can come from having work done
on it at some point in time. Generally, there are two kinds of
energy in mechanical systems, potential and kinetic.
Potential energy is due to the position of the object and
kinetic energy is due to its movement.
For example, an object set in motion can overcome a certain amount of
resistance before being brought to rest, and the energy which the
object has on account of its motion is used up in overcoming the
resistance, bring the object to rest. Fly wheels on engines
both receive and give up energy and thus cause the
energy to return more smoothly throughout the stroke.
Elevated weights have power to do work on
account of their elevated position, as in various types of hammers,
etc.

Complete Table of Contents
- 1 Physical Principles
- 1.1 Force and Torque
- 1.1.1 Force
- 1.1.2 Torque
- 1.2 Motion
- 1.2.1 Motion Along a Straight Path
- 1.2.2 Linear Motion in Space
- 1.2.3 Motion of a Rigid Body in a Plane
- 1.3 Newton's Law of Motion
- 1.3.1 Newton's First Law
- 1.3.2 Newton's Second Law
- 1.4 Momentum and Conservation of Momentum
- 1.4.1 Impulse
- 1.4.2 Momentum
- 1.4.3 Conservation of Momentum
- 1.5 Work, Power and Energy
- 1.5.1 Work
- 1.5.2 Power
- 1.5.3 Energy
- 2 Mechanisms and Simple Machines
- 3 More on Machines and Mechanisms
- 4 Basic Kinematics of Constrained Rigid Bodies
- 5 Planar Linkages
- 6 Cams
- 7 Gears
- 8 Other Mechanisms
- Index
- References




sfinger@ri.cmu.edu
| 
